Imputation • COINr

Introduction

Imputation is the process of estimating missing data points. To get started with imputation, a reasonable first step is to see how much missing data we have in the data set. We begin by building the example coin, up the point of assembling the coin, but not any further:

library(COINr)

ASEM <- build_example_coin(up_to = "new_coin", quietly = TRUE)

To check missing data, the get_data_avail() function can be used. It can output to either the coin or to a list – here we output to a list to readily display the results.

l_avail <- get_data_avail(ASEM, dset = "Raw", out2 = "list")

The output list has data availability by unit:

head(l_avail$Summary)
#>    uCode N_missing N_zero N_miss_or_zero Dat_Avail  Non_Zero
#> 31   AUS         0      3              3 1.0000000 0.9387755
#> 1    AUT         0      2              2 1.0000000 0.9591837
#> 2    BEL         0      2              2 1.0000000 0.9591837
#> 32   BGD         6      1              7 0.8775510 0.9767442
#> 3    BGR         0      0              0 1.0000000 1.0000000
#> 33   BRN        10      2             12 0.7959184 0.9487179

The lowest data availability by unit is:

min(l_avail$Summary$Dat_Avail)
#> [1] 0.7959184

We can also check data availability by indicator. This is done by calling get_stats():

df_avail <- get_stats(ASEM, dset = "Raw", out2 = "df")

head(df_avail[c("iCode", "N.Avail", "Frc.Avail")], 10)
#>       iCode N.Avail Frc.Avail
#> 1       LPI      51     1.000
#> 2   Flights      51     1.000
#> 3      Ship      51     1.000
#> 4      Bord      51     1.000
#> 5      Elec      51     1.000
#> 6       Gas      51     1.000
#> 7  ConSpeed      43     0.843
#> 8     Cov4G      51     1.000
#> 9     Goods      51     1.000
#> 10 Services      51     1.000

By indicator, the minimum data availability is:

min(df_avail$Frc.Avail)
#> [1] 0.843

With missing data, several options are available:

Leave it as it is and aggregate anyway (there is also the option for data availability thresholds during aggregation - see Aggregation)
Consider removing indicators that have low data availability (this has to be done manually because it affects the structure of the index)
Consider removing units that have low data availability (see Unit Screening)
Impute missing data

These options can also be combined. Here, we focus on the option of imputation.

Data frames

The Impute() function is a flexible function that imputes missing data in a data set using any suitable function that can be passed to it. In fact, Impute() is a generic, and has methods for coins, data frames, numeric vectors and purses.

Let’s begin by examining the data frame method of Impute(), since it is easier to see what’s going on. We will use a small data frame which is easy to visualise:

# some data to use as an example
# this is a selected portion of the data with some missing values
df1 <-  ASEM_iData[37:46, 36:39]
print(df1, row.names = FALSE)
#>    Pat CultServ CultGood Tourist
#>   23.7  0.13405       NA  11.519
#>  583.5  2.20754   16.182  24.040
#>    3.6  0.05780    0.985   6.509
#>  249.8  1.79800       NA  17.242
#>     NA       NA       NA   3.315
#>   64.2  1.15292    7.555  26.757
#>    0.3  0.00266    0.046   0.404
#>     NA  0.08905       NA   2.907
#>   46.5  0.34615    1.213   3.370
#>    7.2  0.03553    1.256   0.966

In the simplest case, imputation can be performed column-wise, i.e. by imputing each indicator one at a time:

Impute(df1, f_i = "i_mean")
#>       Pat  CultServ CultGood Tourist
#> 37  23.70 0.1340500   4.5395  11.519
#> 38 583.50 2.2075400  16.1820  24.040
#> 39   3.60 0.0578000   0.9850   6.509
#> 40 249.80 1.7980000   4.5395  17.242
#> 41 122.35 0.6470778   4.5395   3.315
#> 42  64.20 1.1529200   7.5550  26.757
#> 43   0.30 0.0026600   0.0460   0.404
#> 44 122.35 0.0890500   4.5395   2.907
#> 45  46.50 0.3461500   1.2130   3.370
#> 46   7.20 0.0355300   1.2560   0.966

Here, the “Raw” data set has been imputed by substituting missing values with the mean of the non-NA values for each column. This is performed by setting f_i = "i_mean". The f_i argument refers to a function that imputes a numeric vector - in this case the built-in i_mean() function:

# demo of i_mean() function, which is built in to COINr
x <- c(1,2,3,4, NA)
i_mean(x)
#> [1] 1.0 2.0 3.0 4.0 2.5

The key concept here is that the simple function i_mean() is applied by Impute() to each column. This idea of passing simpler functions is used in several key COINr functions, and allows great flexibility because more sophisticated imputation methods can be used from other packages, for example.

In COINr there are currently four basic imputation functions which impute a numeric vector:

i_mean(): substitutes missing values with the mean of the remaining values
i_median(): substitutes missing values with the median of the remaining values (this will be more robust to outliers)
i_mean_grp(): substitutes missing values with the mean of a subset of the remaining values, defined by a separate grouping vector
i_median_grp(): substitutes missing values with the mean of a subset of the remaining values, defined by a separate grouping vector

These are very simple imputation methods, but more sophisticated options can be used by calling functions from other packages. The group imputation functions above are useful in an indicator context: for example in country-level indicator analysis we can substitute missing values by the mean/median within the same GDP/capita group, which is often a better approach than a flat mean across all countries. Obviously this is context-dependent however.

For now let’s explore the options native to COINr. We can also apply the i_median() function in the same way to substitute with the indicator median. Adding a little complexity, we can also impute by mean or median, but within unit (row) groups. Let’s assume that the first five rows in our data frame belong to a group “a”, and the remaining five to a different group “b”. In practice, these could be e.g. GDP, population or wealth groups for countries - we might hypothesise that it is better to replace NA values with the median inside a group, rather than the overall median, because countries within groups are more similar.

To do this on a data frame we can use the i_median_grp() function, which requires an additional argument f: a grouping variable. This is passed through Impute() using the f_i_para argument which takes any additional parameters top f_i apart from the data to be imputed.

# row grouping
groups <- c(rep("a", 5), rep("b", 5))

# impute
dfi2 <- Impute(df1, f_i = "i_median_grp", f_i_para = list(f = groups))

# display
print(dfi2, row.names = FALSE)
#>     Pat CultServ CultGood Tourist
#>   23.70 0.134050   8.5835  11.519
#>  583.50 2.207540  16.1820  24.040
#>    3.60 0.057800   0.9850   6.509
#>  249.80 1.798000   8.5835  17.242
#>  136.75 0.966025   8.5835   3.315
#>   64.20 1.152920   7.5550  26.757
#>    0.30 0.002660   0.0460   0.404
#>   26.85 0.089050   1.2345   2.907
#>   46.50 0.346150   1.2130   3.370
#>    7.20 0.035530   1.2560   0.966

The f_i_para argument requires a named list of additional parameter values. This allows functions of any complexity to be passed to Impute(). By default, Impute() applies f_i to each column of data, so f_i is expected to take a numeric vector as its first input, and specifically have the format function(x, f_i_para) where x is a numeric vector and ... are further arguments. This means that the first argument of f_i must be called “x”. To use functions that don’t have x as a first argument, you would have to write a wrapper function.

Other than imputing by column, we can also impute by row. This only really makes sense if the indicators are on a common scale, i.e. if they are normalised first (or perhaps if they already share the same units). To impute by row, set impute_by = "row". In our example data set we have indicators on rather different scales. Let’s see what happens if we impute by row mean but don’t normalise:

Impute(df1, f_i = "i_mean", impute_by = "row", normalise_first = FALSE)
#>           Pat CultServ  CultGood Tourist
#> 37  23.700000  0.13405 11.784350  11.519
#> 38 583.500000  2.20754 16.182000  24.040
#> 39   3.600000  0.05780  0.985000   6.509
#> 40 249.800000  1.79800 89.613333  17.242
#> 41   3.315000  3.31500  3.315000   3.315
#> 42  64.200000  1.15292  7.555000  26.757
#> 43   0.300000  0.00266  0.046000   0.404
#> 44   1.498025  0.08905  1.498025   2.907
#> 45  46.500000  0.34615  1.213000   3.370
#> 46   7.200000  0.03553  1.256000   0.966

This imputes some silly values, particularly in “CultGood”, because “Pat” has much higher values. Clearly this is not a sensible strategy, unless all indicators are on the same scale. We can however normalise first, impute, then return indicators to their original scales:

Impute(df1, f_i = "i_mean", impute_by = "row", normalise_first = TRUE, directions = rep(1,4))
#>          Pat CultServ  CultGood Tourist
#> 37  23.70000 0.134050  2.850908  11.519
#> 38 583.50000 2.207540 16.182000  24.040
#> 39   3.60000 0.057800  0.985000   6.509
#> 40 249.80000 1.798000 10.163326  17.242
#> 41  64.72133 0.246215  1.828412   3.315
#> 42  64.20000 1.152920  7.555000  26.757
#> 43   0.30000 0.002660  0.046000   0.404
#> 44  39.42134 0.089050  1.128411   2.907
#> 45  46.50000 0.346150  1.213000   3.370
#> 46   7.20000 0.035530  1.256000   0.966

This additionally required to specify the directions argument because we need to know which direction each indicator runs in (whether they are positive or negative indicators). In our case all indicators are positive. See the vignette on Normalisation for more details on indicator directions.

The values imputed in this way are more realistic. Essentially we are replacing each missing value with the average (normalised) score of the other indicators, for a given unit. However this also only makes sense if the indicators/columns are similar to one another: high values of one would likely imply high values in the other.

Behind the scenes, setting normalise_first = TRUE first normalises each column using a min-max method, then performs the imputation, then returns the indicators to the original scales using the inverse transformation. Another approach which gives more control is to simply run Normalise() first, and work with the normalised data from that point onwards. In that case it is better to set normalise_first = FALSE, since by default if impute_by = "row" it will be set to TRUE.

As a final point on data frames, we can set impute_by = "df" to pass the entire data frame to f_i, which may be useful for more sophisticated multivariate imputation methods. But what’s the point of using Impute() then, you may ask? First, because when imputing coins, we can impute by indicator groups (see next section); and second, Impute() performs some checks to ensure that non-NA values are not altered.

Coins

Imputing coins is similar to imputing data frames because the coin method of Impute() calls the data frame method. Please read that section first if you have not already done so. However, for coins there are some additional function arguments.

In the simple case we impute a named data set dset using the function f_i: e.g. if we want to impute the “Raw” data set using indicator median values:

ASEM <- Impute(ASEM, dset = "Raw", f_i = "i_mean")
#> Written data set to .$Data$Imputed

ASEM
#> --------------
#> A coin with...
#> --------------
#> Input:
#>   Units: 51 (AUS, AUT, BEL, ...)
#>   Indicators: 49 (Goods, Services, FDI, ...)
#>   Denominators: 4 (Area, Energy, GDP, ...)
#>   Groups: 4 (GDP_group, GDPpc_group, Pop_group, ...)
#> 
#> Structure:
#>   Level 1 Indicator: 49 indicators (FDI, ForPort, Goods, ...) 
#>   Level 2 Pillar: 8 groups (ConEcFin, Instit, P2P, ...) 
#>   Level 3 Sub-index: 2 groups (Conn, Sust) 
#>   Level 4 Index: 1 groups (Index) 
#> 
#> Data sets:
#>   Raw (51 units)
#>   Imputed (51 units)

Here, Impute() extracts the “Raw” data set as a data frame, imputes it using the data frame method (see previous section), then saves it as a new data set in the coin. Here, the data set is called “Imputed” but can be named otherwise using the write_to argument.

We can also impute by group using a grouped imputation function. Since unit groups are stored within the coin (variables labelled as “Group” in iMeta), these can be called directly using the use_group argument (without having to specify the f_i_para argument):

ASEM <- Impute(ASEM, dset = "Raw", f_i = "i_mean_grp", use_group = "GDP_group", )
#> Written data set to .$Data$Imputed
#> (overwritten existing data set)

This has imputed each indicator using its GDP group mean.

Row-wise imputation works in the same way as with a data frame, by setting impute_by = "row". However, this is particularly useful in conjunction with the group_level argument. If this is specified, rather than imputing across the entire row of data, it splits rows into indicator groups, using the structure of the index. For example:

ASEM <- Impute(ASEM, dset = "Raw", f_i = "i_mean", impute_by = "row",
               group_level = 2, normalise_first = TRUE)
#> Written data set to .$Data$Imputed
#> (overwritten existing data set)

Here, the group_level argument specifies which level-grouping of the indicators to use. In the ASEM example here, we are using level 2 groups, so it is substituting missing values with the average normalised score within each sub-pillar (in the ASEM example level 2 is called “sub-pillars”).

Imputation in this way has an important relationship with aggregation. This is because if we don’t impute, then in the aggregation step, if we take the mean of a group of indicators, and there is a NA present, this value is excluded from the mean calculation. Doing this is mathematically equivalent to assigning the mean to that missing value and then taking the mean of all of the indicators. This is sometimes known as “shadow imputation”. Therefore, one reason to use this imputation method is to see which values are being implicitly assigned as a result of excluding missing values from the aggregation step.

Last we can see an example of imputation by data frame, with the option impute_by = "row". Recall that this option requires that the function f_i accepts and returns entire data frames. This is suitable for more sophisticated multivariate imputation methods. Here we’ll use a basic implementation of the Expectation Maximisation (EM) algorithm from the Amelia package.

Since COINr requires that the first argument of f_i is called x, and the relevant Amelia function doesn’t satisfy this requirement, we have write a simple wrapper function that acts as an intermediary between COINr and Amelia. This also gives us the chance to specify some other function arguments that are necessary.

# this function takes a data frame input and returns an imputed data frame using amelia
i_EM <- function(x){
  # impute
  amOut <- Amelia::amelia(x, m = 1, p2s = 0, boot.type = "none")
  # return imputed data
  amOut$imputations[[1]]
}

Now armed with our new function, we just call that from Impute(). We don’t need to specify f_i_para because these arguments are already specified in the intermediary function.

# impute raw data set
coin <- Impute(coin, dset = "Raw", f_i = i_EM, impute_by = "df", group_level = 2)

This has now passed each group of indicators at level 2 as data frames to Amelia, which has imputed each one and passed them back.

Purses

Purse imputation is very similar to coin imputation, because by default the purse method of Impute() imputes each coin separately. There is one exception to this: if f_i = "impute_panel", the data sets inside the purse are imputed past/future values in the same time series, using the impute_panel() function. In this case, coins are not imputed individually, but treated as a single data set. When f_i = "impute_panel", you can optionally set the values of the impute_panel() arguments using the f_i_para argument of Impute().

It is difficult to show this working without a contrived example, so let’s contrive one. We take the example panel data set ASEM_iData_p, and introduce a missing value NA in the indicator “LPI” for unit “GB”, for year 2021.

# copy
dfp <- ASEM_iData_p

# create NA for GB in 2021
dfp$LPI[dfp$uCode == "GBR" & dfp$Time == 2021] <- NA

This data point has a value for the previous year, 2020. Let’s see what it is:

dfp$LPI[dfp$uCode == "GBR" & dfp$Time == 2020]
#> [1] 4.167858

Now let’s build the purse and impute the raw data set.

# build purse
ASEMp <- new_coin(dfp, ASEM_iMeta, split_to = "all", quietly = TRUE)

# impute raw data using latest available value
ASEMp <- Impute(ASEMp, dset = "Raw", f_i = "impute_panel")
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed

Now we check whether our imputed point is what we expect: we would expect that our NA is now replaced with the 2020 value as found previously. To get at the data we can use the get_data() function.

get_data(ASEMp, dset = "Imputed", iCodes = "LPI", uCodes = "GBR")
#>     Time uCode      LPI
#> 30  2018   GBR 4.069669
#> 81  2019   GBR 4.120399
#> 132 2020   GBR 4.167858
#> 183 2021   GBR 4.167858
#> 234 2022   GBR 4.118561

And indeed this corresponds to what we expect.

We can also optionally change parameters in impute_panel(). Currently it is possible to change the "imp_type" and "max_time" parameters. To do this, we use f_i_para argument of Impute() to pass these parameters.

To understand this better, it’s useful to consider that in panel data, each unit-indicator pair has a time series which describes the evolution of that indicator, for that unit. So keeping our previous example with GBR and the LPI indicator, our time series looks like this:

# make purse with fresh panel data
ASEMp <- new_coin(ASEM_iData_p, ASEM_iMeta, split_to = "all", quietly = TRUE)

# extract and plot time series for GBR for indicator LPI
df_plot <- get_data(ASEMp, dset = "Raw", iCodes = "LPI", uCodes = "GBR")
plot(df_plot$Time, df_plot$LPI, type = "b", xlab = "Year", ylab = "LPI for GBR")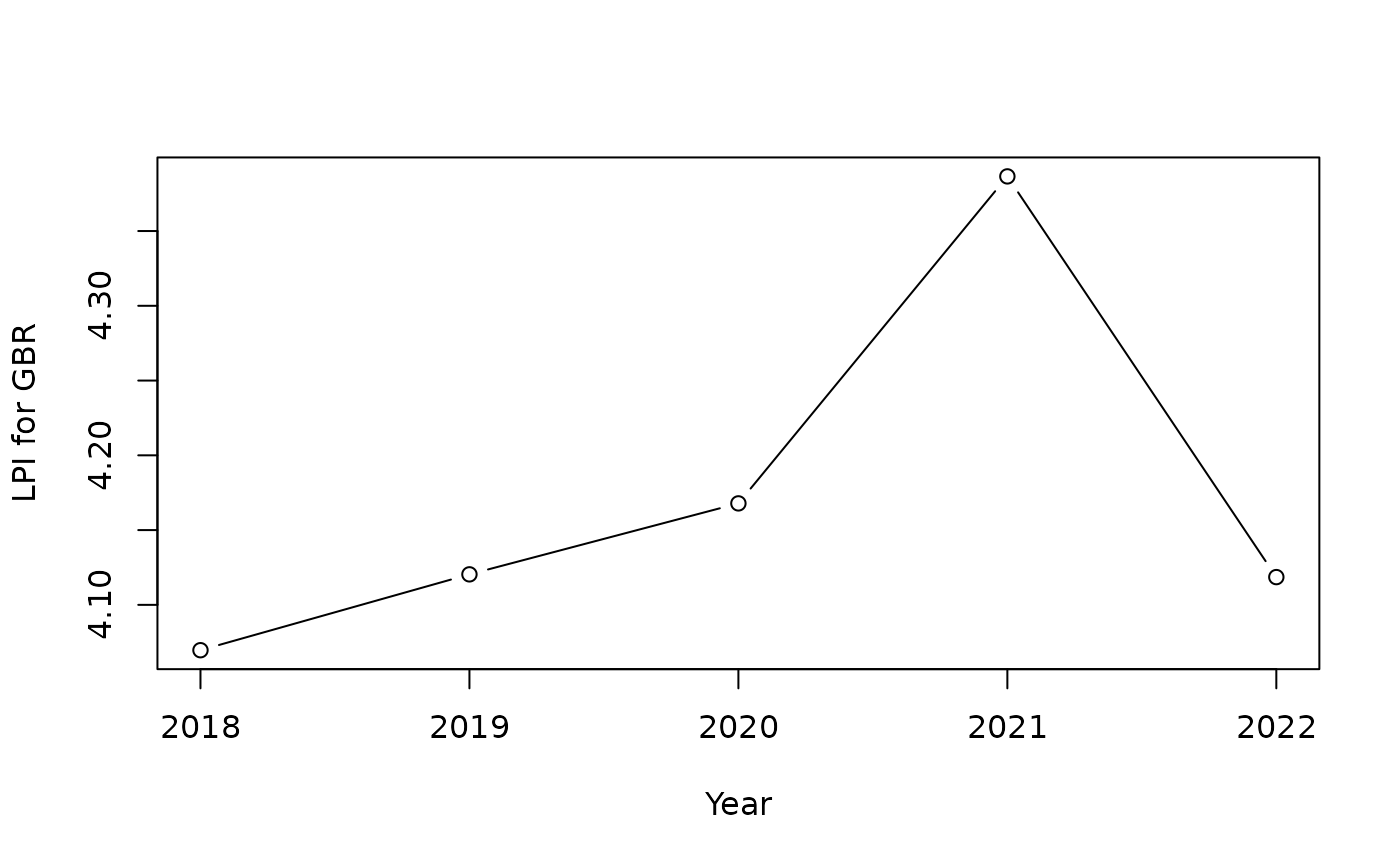

Now let’s demonstrate imputing this time series with adjusting the imputation method. First, we have to artificially create a missing value for the purposes of this demo. We will do this by removing the 2021 value in the input data, then recreating the purse object (similar to previous example). We will then plot the series again to check.

# copy
dfp <- ASEM_iData_p

# create NA for GB in 2021
dfp$LPI[dfp$uCode == "GBR" & dfp$Time == 2021] <- NA

# make purse with fresh panel data
ASEMp <- new_coin(dfp, ASEM_iMeta, split_to = "all", quietly = TRUE)

# extract and plot time series for GBR for indicator LPI
df_plot <- get_data(ASEMp, dset = "Raw", iCodes = "LPI", uCodes = "GBR")
plot(df_plot$Time, df_plot$LPI, type = "b", xlab = "Year", ylab = "LPI for GBR")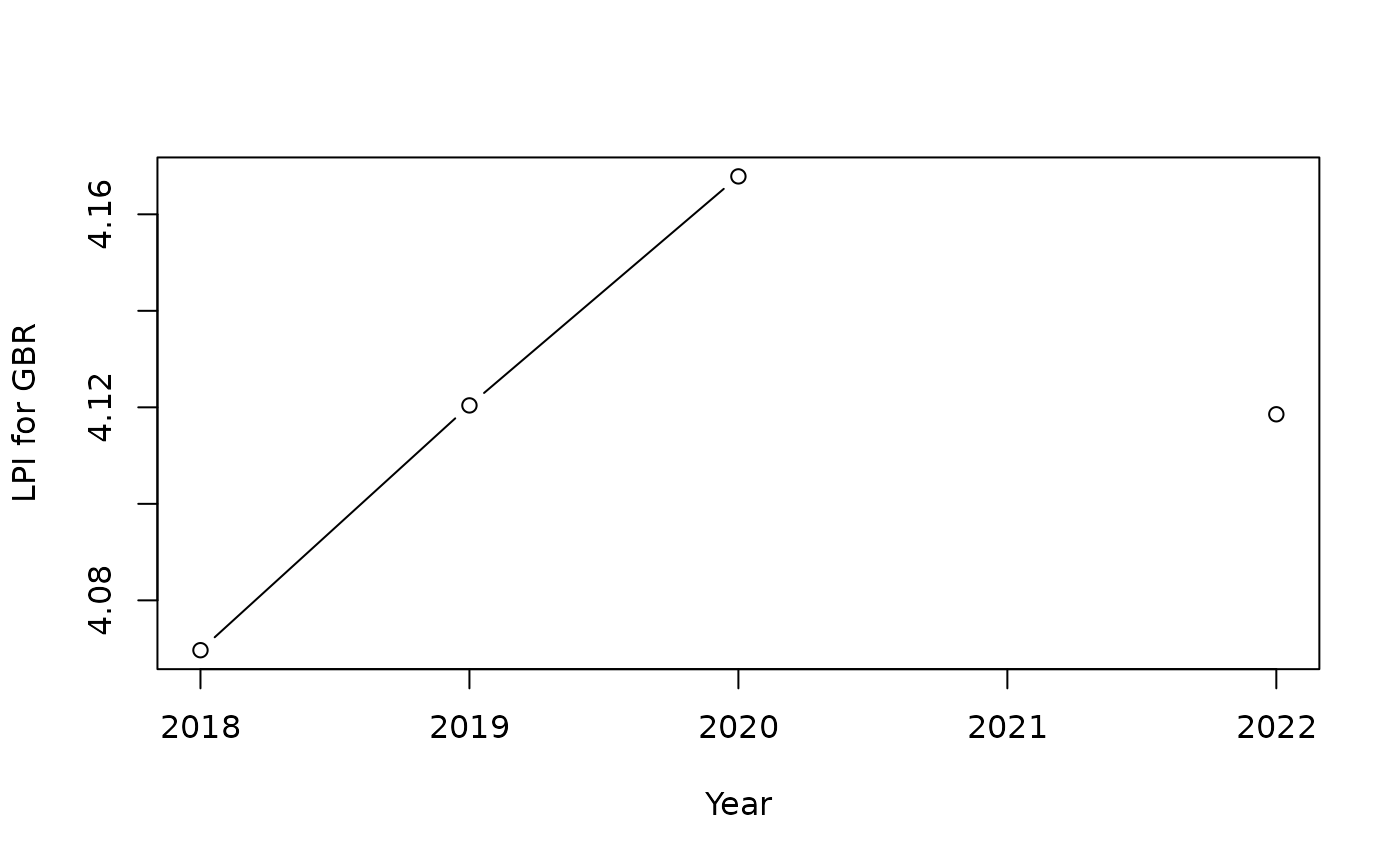

The plot confirms we have removed the data point. Now, we will impute the missing point in 2021 using linear interpolation. This is achieved by setting the imp_type argument to “linear”, via the f_i_para argument, as follows:

ASEMp <- Impute(ASEMp, dset = "Raw", f_i = "impute_panel", f_i_para = list(imp_type = "linear"))
#> NOTE: cannot impute for unit BGD and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit BGD and iCode TBTs because all NA values.
#> NOTE: cannot impute for unit BGD and iCode Pat because all NA values.
#> NOTE: cannot impute for unit BGD and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit BGD and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit BGD and iCode RDExp because all NA values.
#> NOTE: cannot impute for unit BRN and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit BRN and iCode ForPort because all NA values.
#> NOTE: cannot impute for unit BRN and iCode Pat because all NA values.
#> NOTE: cannot impute for unit BRN and iCode CultServ because all NA values.
#> NOTE: cannot impute for unit BRN and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit BRN and iCode Palma because all NA values.
#> NOTE: cannot impute for unit BRN and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit BRN and iCode FemLab because all NA values.
#> NOTE: cannot impute for unit BRN and iCode PrivDebt because all NA values.
#> NOTE: cannot impute for unit BRN and iCode RDExp because all NA values.
#> NOTE: cannot impute for unit CHN and iCode NEET because all NA values.
#> NOTE: cannot impute for unit ESP and iCode CultServ because all NA values.
#> NOTE: cannot impute for unit IDN and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit ITA and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit JPN and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit KAZ and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit KAZ and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit KHM and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit KHM and iCode ForPort because all NA values.
#> NOTE: cannot impute for unit KHM and iCode Pat because all NA values.
#> NOTE: cannot impute for unit KHM and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit KHM and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit KHM and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit KOR and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit KOR and iCode Palma because all NA values.
#> NOTE: cannot impute for unit KOR and iCode NEET because all NA values.
#> NOTE: cannot impute for unit LAO and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit LAO and iCode ForPort because all NA values.
#> NOTE: cannot impute for unit LAO and iCode Pat because all NA values.
#> NOTE: cannot impute for unit LAO and iCode CultServ because all NA values.
#> NOTE: cannot impute for unit LAO and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit LAO and iCode PrimEner because all NA values.
#> NOTE: cannot impute for unit LAO and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit LAO and iCode RDExp because all NA values.
#> NOTE: cannot impute for unit MLT and iCode Palma because all NA values.
#> NOTE: cannot impute for unit MMR and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit MMR and iCode Tariff because all NA values.
#> NOTE: cannot impute for unit MMR and iCode Pat because all NA values.
#> NOTE: cannot impute for unit MMR and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit MMR and iCode Palma because all NA values.
#> NOTE: cannot impute for unit MMR and iCode TertGrad because all NA values.
#> NOTE: cannot impute for unit MMR and iCode FemLab because all NA values.
#> NOTE: cannot impute for unit MMR and iCode RDExp because all NA values.
#> NOTE: cannot impute for unit MNG and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit MNG and iCode Tariff because all NA values.
#> NOTE: cannot impute for unit MNG and iCode PubDebt because all NA values.
#> NOTE: cannot impute for unit MYS and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit NZL and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit NZL and iCode Palma because all NA values.
#> NOTE: cannot impute for unit PAK and iCode ConSpeed because all NA values.
#> NOTE: cannot impute for unit SGP and iCode Poverty because all NA values.
#> NOTE: cannot impute for unit SGP and iCode Palma because all NA values.
#> NOTE: cannot impute for unit THA and iCode Tariff because all NA values.
#> NOTE: cannot impute for unit VNM and iCode Pat because all NA values.
#> NOTE: cannot impute for unit VNM and iCode CultServ because all NA values.
#> NOTE: cannot impute for unit VNM and iCode CultGood because all NA values.
#> NOTE: cannot impute for unit VNM and iCode TertGrad because all NA values.
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed
#> Written data set to .$Data$Imputed

Recall that by doing this, we are imputing all time series in the purse in the same way. The warning messages above come from the fact that some time series have all NA values, so cannot be imputed in any way.

We will now check to see how the imputation went for our selected time series. We extract the time series from the Imputed data set, and plot it.

# extract and plot time series for GBR for indicator LPI
df_plot <- get_data(ASEMp, dset = "Imputed", iCodes = "LPI", uCodes = "GBR")
plot(df_plot$Time, df_plot$LPI, type = "b", xlab = "Year", ylab = "LPI for GBR")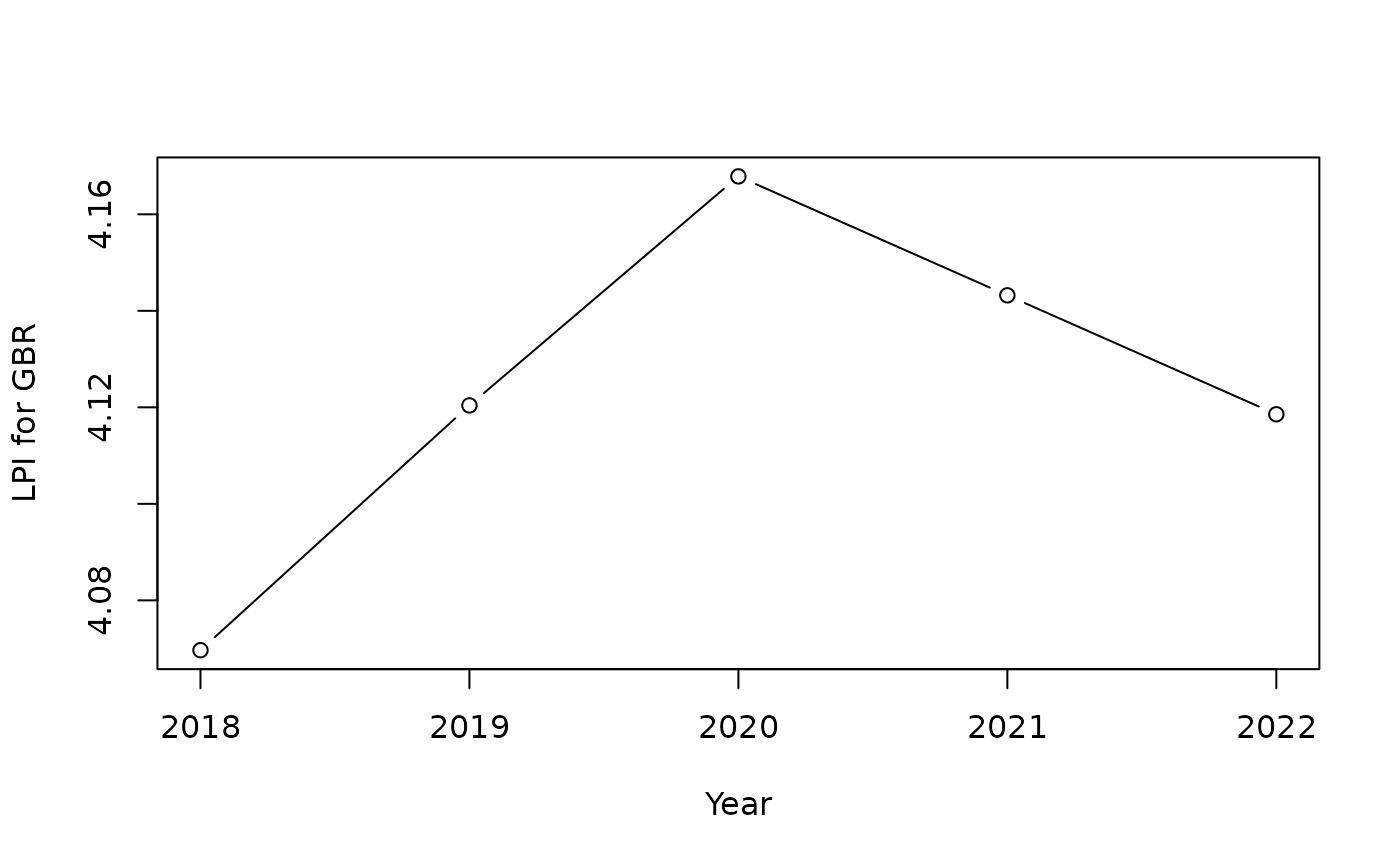

The plot shows that the 2021 value has been imputed, as expected, by drawing a straight line from 2020 to 2022.

Note that if you have any time series with only one non-NA observation, the “linear” method will throw an error because linear imputation cannot work with only one point. In this case, you can set imp_type = "linear-constant"), which will use linear regression where possible, but will revert to the “constant” method for any series with only one known observation.

Consider that the impute_panel() function allows fairly basic time series imputation using the functionalities of stats::approx(). If you need more sophisticated imputation, this would either have to be done outside of COINr, or implemented using a Custom() operation.